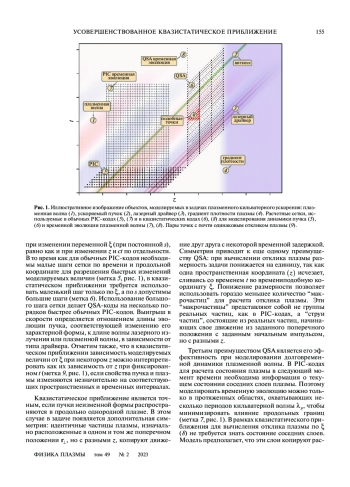
Квазистатическое приближение является эффективным методом моделирования плазменного кильватерного ускорения, но оно становится неточным, если в сильнонелинейной волне отдельные частицы плазмы смещаются на большое расстояние в продольном направлении, если в плазме есть волны с ненулевой групповой скоростью или резкие градиенты плотности, или если форма пучка быстро меняется. Работа посвящена расширению квазистатического приближения, лишенному многих его ограничений и сохраняющему его основные преимущества – скорость вычислений и пониженную размерность расчетной области. В новом подходе учитывается обмен информацией между соседними слоями плазмы. В работе сформулирована физическая модель и описана ее численная реализация. Результаты моделирования сравниваются с существующими аналитическими решениями и другими кодами.
Идентификаторы и классификаторы
Ускорение частиц в плазме, и в частности кильватерное ускорение, – перспективное направление развития ускорителей [1]. В этом методе драйвер (пучок заряженных частиц или короткий лазерный импульс) распространяется в плазме и возбуждает в ней ленгмюровскую волну, которая способна ускорять другой пучок частиц, называемый витнессом. Драйвер и витнесс движутся почти со скоростью света, поэтому обмен энергией между ними посредством плазмы может быть длительным и эффективным.
Список литературы
1. Albert F., Couprie M.E., Debus A., Downer M.C., Faure J., Flacco A., Gizzi L.A., Grismayer T., Huebl A., Joshi C., Labat M., Leemans W.P., Maier A.R., Mangles S.P.D., Mason P., Mathieu F., Muggli P., Nishiuchi M., Oster-hoff J., Rajeev P.P., Schramm U., Schreiber J., Tho-mas A.G.R., Vay J.-L., Vranic M., Zeil K. // New J. Phys. 2021. V. 23. P. 031101. DOI: 10.1088/1367-2630/abcc62 EDN: YPZVJX
2. Vay J.-L., Lehe R. // Rev. Accelerator Science Technology. 2016. V. 9. P. 165. DOI: 10.1142/S1793626816300085
3. Lotov K.V. // Nuclear Instr. Methods A. 1998. V. 410. P. 461. DOI: 10.1016/S0168-9002(98)00178-8 EDN: LERSWH
4. Burdakov A.V., Kudryavtsev A.M., Logatchov P.V., Lo-tov K.V., Petrenko A.V., Skrinsky A.N. // Plasma Phys. Rep. 2005. V. 31. P. 292. [Бурдаков А.В., Кудряв-цев А.М., Логачев П.В., Лотов К.В., Петренко А.В., Скринский А.Н. // Физика плазмы, 2005, Т. 31, C. 327–335.]. DOI: 10.1134/1.1904145 EDN: LJICWR
5. Schroeder C.B., Esarey E., Geddes C.G.R., Benedetti C., Leemans W.P. // Phys. Rev. ST Accel. Beams. 2010. V. 13. P. 101301. DOI: 10.1103/PhysRevSTAB.13.101301 EDN: OKRVXJ
6. Nakajima K., Deng A., Zhang X., Shen B., Liu J., Li R., Xu Z., Ostermayr T., Petrovics S., Klier C., Iqbal K., Ruhl H., Tajima T. // Phys. Rev. ST Accel. Beams. 2011. V. 14. P. 091301. DOI: 10.1103/PhysRevSTAB.14.091301 EDN: PGQGGZ
7. Schroeder C.B., Esarey E., Leemans W.P. // Phys. Rev. ST Accel. Beams, 2012. V. 15. P. 051301. DOI: 10.1103/PhysRevSTAB.15.051301
8. Vay J.-L. // Phys. Rev. Lett. 2007. V. 98. P. 130405. DOI: 10.1103/PhysRevLett.98.130405
9. Vay J.-L., Geddes C.G.R., Cormier-Michel E., Gro-te D.P. // J. Computational Phys. 2011. V. 230. P. 5908. DOI: 10.1016/j.jcp.2011.04.003 EDN: OLGQVV
10. Sprangle P., Esarey E., Ting A. // Phys. Rev. Lett. 1990. V. 64. P. 2011. DOI: 10.1103/PhysRevLett.64.2011
11. Mora P., Antonsen T.M. // Phys. Plasmas. 1997. V. 4. P. 217. DOI: 10.1063/1.872134 EDN: LOCQCJ
12. Jain N., Palastro J., Antonsen T.M., Mori W.B., An W. // Phys. Plasmas, 2015. V. 22. P. 023103. DOI: 10.1063/1.4907159 EDN: YCIFDF
13. Sosedkin A.P., Lotov K.V. // Nuclear Instr. Methods A. 2016. V. 829. P. 350. DOI: 10.1016/j.nima.2015.12.032 EDN: WPETQD
14. An W., Decyk V.K., Mori W.B., Antonsen Jr. T.M. // J. Computational Phys. 2013. V. 250. P. 165. DOI: 10.1016/j.jcp.2013.05.020 EDN: RJYLAX
15. Mehrling T., Benedetti C., Schroeder C.B., Osterhoff J. // Plasma Phys. Control. Fusion, 2014. V. 56. P. 084012. DOI: 10.1088/0741-3335/56/8/084012 EDN: USUVTL
16. Pukhov A., Farmer J.P. // Phys. Rev. Lett. 2018. V. 121. P. 264801. DOI: 10.1103/PhysRevLett.121.264801 EDN: XAFFCR
17. Zhu W., Palastro J.P., Antonsen T.M. // Phys. Plasmas, 2012. V. 19. P. 033105. DOI: 10.1063/1.3691837 EDN: NJKPWF
18. Huang C., Decyk V.K., Ren C., Zhou M., Lu W., Mo-ri W.B., Cooley J.H., Antonsen Jr.T.M., Katsouleas T. // J. Computational Phys. 2006. V. 217. P. 658. DOI: 10.1016/j.jcp.2006.01.039 EDN: MFLTAH
19. Спицын Р.И. Магистерская дисс. Новосибирский государственный университет, 2016. https://www.inp.nsk.su/~dep_plasma/dip/Spitsyn_m.pdf.
20. Terzani D., Benedetti C., Schroeder C.B., Esarey E. // Phys. Plasmas. 2021. V. 28. P. 063105. DOI: 10.1063/5.0050580 EDN: CDBBCK
21. Sprangle P., Esarey E., Krall J., Joyce G., Phys. Rev. Lett., 1992. V. 69. P. 2200. DOI: 10.1103/PhysRevLett.69.2200 EDN: XOQLLG
22. Esarey E., Sprangle P., Krall J., Ting A., Joyce G. // Phys. Fluids B. 1993. V. 5. P. 2690. DOI: 10.1063/1.860707
23. Lotov K.V. // Phys. Plasmas. 1998. V. 5. P. 785. DOI: 10.1063/1.872765 EDN: ACEFHD
24. Zgadzaj R., Silva T., Khudyakov V.K., Sosedkin A., Al-len J., Gessner S., Li Z., Litos M., Vieira J., Lotov K.V., Hogan M.J., Yakimenko V., Downer M.C. // Nature Comm. 2020. V. 11. P. 4753. -w. DOI: 10.1038/s41467-020-18490 EDN: KVNNAG
25. Khudiakov V.K., Lotov K.V., Downer M.C. // Plasma Phys. Control. Fusion. 2022. V. 64. P. 045003. DOI: 10.1088/1361-6587/ac4523 EDN: DRFIQT
26. Benedetti C., Schroeder C.B., Geddes C.G.R., Esarey E., Leemans W.P. // Plasma Phys. Control. Fusion. 2018. V. 60. P. 014002. DOI: 10.1088/1361-6587/aa8977
27. Zhu W., Palastro J.P., Antonsen T.M. // Phys. Plasmas. 2013. V. 20. P. 073103. DOI: 10.1063/1.4813245 EDN: RNMOXF
28. Lotov K.V. // Phys. Rev. ST Accel. Beams. 2003. V. 6. P. 061301. DOI: 10.1103/PhysRevSTAB.6.061301 EDN: LHVYKV
29. https://lcode.info/.
30. See the LCODE manual at https://lcode.info/site-files/manual.pdf.
31. Crank J., Nicolson P. // Mathematical Proceed. Cambridge Philosophical Soc. 1947. V. 43. P. 50. DOI: 10.1017/S0305004100023197
32. Peaceman D.W., Rachford H.H. // J. Soc. Industrial Applied Math. 1955. V. 3. P. 28. DOI: 10.1137/0103003
33. Douglas J. // J. Soc. Industrial Applied Math. 1955. V. 3. P. 42. DOI: 10.1137/0103004
34. Esarey E., Leemans W.P. // Phys. Rev. E. 1999. V. 59. P. 1082. DOI: 10.1103/PhysRevE.59.1082 EDN: LQDVKN
35. Lehe R., Kirchen M., Andriyash I.A., Godfrey B.B., Vay J.-L. // Computer Phys. Communications. 2016. V. 203. P. 66. DOI: 10.1016/j.cpc.2016.02.007 EDN: YDJQUG
36. Luo J., Chen M., Zhang G.-B., Yuan T., Yu J.-Y., Shen Z.-C., Yu L.-L., Weng S.-M., Schroeder C. B., Esa-rey E. // Phys. Plasmas. 2016. V. 23. P. 103112. DOI: 10.1063/1.4966047 EDN: XUONYF
37. Massimo F., Beck A., Derouillat J., Grech M., Lobet M., Perez F., Zemzemi I., Specka A. // Plasma Phys. Control. Fusion. 2019. V. 61. P. 124001. cf. DOI: 10.1088/1361-6587/ab49
38. Terzani D., Londrillo P. // Computer Phys. Communicat. 2019. V. 242. P. 49. DOI: 10.1016/j.cpc.2019.04.007 EDN: ZXVFHT
39. Pukhov A., Meyer-ter-Vehn J. // Appl. Phys. B, 2002. V. 74. P. 355. DOI: 10.1007/s003400200795 EDN: LWHOKF
40. Malka V. // Phys. Plasmas, 2012. V. 19. P. 055501. DOI: 10.1063/1.3695389 EDN: PGTIHJ
41. Esarey E., Schroeder C.B., Leemans W.P. // Rev. Mod. Phys. 2009. V. 81. P. 1229. DOI: 10.1103/RevModPhys.81.1229 EDN: MYCXRL
42. Morshed S., Antonsen T.M., Palastro J.P. // Phys. Plasmas, 2010. V. 17. P. 063106. DOI: 10.1063/1.3432685 EDN: URXLTT
43. Tuev P.V., Lotov K.V. Proc. 47th EPS Conference on Plasma Phys. 2021. P. 2.2004. http://ocs.ciemat.es/EPS2021PAP/pdf/P2.2004.pdf.
44. Irkutsk Supercomputer Center of SB RAS (available at: http://ocs.ciemat.es/EPS2021PAP/pdf/P2.2004.pdf).
Выпуск
Другие статьи выпуска
Проведено экспериментальное исследование динамики разряда в постоянном квазиоднородном электрическом поле, инициированного плазменным филаментом, создаваемым фемтосекундным лазерным импульсом. Измерено время развития инициированного разряда (время задержки возникновения разряда относительно лазерного импульса) в зависимости от напряженности постоянного электрического поля в плазменном филаменте и проведено сравнение этой экспериментальной зависимости с результатами численного расчета разрядного процесса в филаменте.
Приводятся результаты первых экспериментов по изучению объемной генерации отрицательных ионов водорода при использовании плотной газодинамической плазмы ЭЦР-разряда, который поддерживался непрерывным микроволновым излучением гиротрона (28 ГГц/5 кВт). ЭЦР водородный разряд зажигался в вакуумной камере, помещенной в магнитное поле, создаваемое системой из двух последовательно соединенных магнитных ловушек. Была проведена оптимизация параметров системы с целью получения максимальной средней плотности тока отрицательных ионов j = 25 мА/см2. Определена область генерации отрицательных ионов, измерены зависимости плотности их тока от давления газа и мощности микроволнового излучения, показана перспективность дальнейшей оптимизации по напряжению экстракции.
Определены и сопоставлены между собой характеристики объемных пылевых структур, создаваемых в трех пылевых ловушках в тлеющем разряде. Устойчивыми в наложенном магнитном поле с индукцией до 2 Тл являются следующие пылевые ловушки: стоячая страта, область сжатия канала тока (внутри специальной диэлектрической вставки), область разряда, находящаяся в сильно неоднородном магнитном поле. Представлены геометрические характеристики объемных пылевых структур и особенности динамики их вращения: продольного и поперечного относительно вектора магнитной индукции размера, угловой скорости, ее продольного градиента в каждой из пылевых ловушек. Проанализированы отличия экспериментально полученных характеристик объемных пылевых структур в сильном магнитном поле в тлеющем и ВЧ-разрядах.
Получена система одномерных многогрупповых уравнений для трех первых моментов функции распределения электронов в области промежуточных и высоких энергий, которая включает в себя уравнения баланса концентрации, плотности потока и плотности потока импульса электронов. Система предназначена для численного моделирования процессов, протекающих с участием быстрых электронов в слабоионизованной холодной плазме.
Рассмотрены особенности экспериментальной работы плазменного релятивистского СВЧ-генератора (ПРГ) Sinus 550-80 при разных значениях концентрации плазмы. Рассмотрены два значения концентрации плазмы, при которых центральные частоты выходного СВЧ-излучения ПРГ были равны 5.1 ГГц и 11.5 ГГц. Численное моделирование демонстрирует снижение концентрации электронов плазмы в результате действия заряда релятивистского электронного пучка (РЭП) при черенковском взаимодействии и возникновение “ионного фона” в течение импульса ПРГ. При низких концентрациях плазмы это может приводить к изменению условий СВЧ-генерации – сопровождаться не только изменением широкополосного излучения на узкополосное, но и снижением мощности излучения. В то же время при больших значениях концентрации плазмы при генерации СВЧ-излучении на высоких частотах средняя амплитуда электрического поля волны практически не меняется в течение импульса РЭП, а излучение остается широкополосным. Анализ результатов экспериментов и численного моделирования подкреплен оценками линейной теории, доказывающей, что при более высоких значениях концентрации плазмы ПРГ работает более устойчиво.
Представлена одномерная газодинамическая модель, позволяющая установить необходимые условия возникновения и характеристики стационарного течения сжимаемой сплошной среды с нелинейной теплопроводностью, примером которой является полностью или частично ионизированная плазма, при наличии локализованного источника тепла заданной мощности.
Обсуждаются механизмы генерации частотных спектров аномального рассеяния в неплотной плазме при СВЧ-нагреве необыкновенной волной на второй гармонике резонанса. Разработанная теория применяется для интерпретации результатов экспериментов по электронному циклотронному резонансном нагреву (ЭЦРН) плазмы на стеллараторе Wendelstein 7-X, в которых наблюдались как стоксовая, так и антистоксовая частотные полосы, смещенные вниз и вверх относительно частоты генератора. Приводится объяснение парадоксального превышения амплитуды антистоксовой компоненты спектра над амплитудой стоксовой компоненты в ряде экспериментов.
Создан симулятор кинетики рециклинга изотопов водорода в плазме для Н-альфа диагностики топливного соотношения в токамаке-реакторе. Симулятор является обобщением на случай смеси изотопов метода, являющегося модификацией для водорода известного метода SXB для определения плотности потока примеси с первой стенки вакуумной камеры в плазму по измерению интенсивности спектральной линии атома или иона, интегральной по длине волны в пределах ширины линии. Симулятор позволяет в режиме реального времени (например, за время 100 мс по требованиям контроля параметров изотопов водорода в демонстрационном токамаке-реакторе ИТЭР) определять параметры топливного соотношения для смеси изотопов водорода дейтерия и трития. Развитый подход позволяет определять плотность потока изотопов водорода с первой стенки в плазму по результатам спектроскопии высокого разрешения линий бальмеровской серии без использования существенных, но трудно интерпретируемых молекулярных спектров водорода. Проведенные расчеты для типичных условий пристеночной плазмы в токамаках-реакторах показали приемлемую точность восстановления плотности потока и топливного отношения в некоторой части операционного пространства работы реактора. Обсуждается место симулятора в более точной и более длительной интерпретации измерений Н-альфа диагностики.
Статистика статьи
Статистика просмотров за 2025 год.
Издательство
- Издательство
- ИОФ РАН
- Регион
- Россия, Москва
- Почтовый адрес
- 119991 ГСП-1, г. Москва, ул. Вавилова, д. 38
- Юр. адрес
- 119991 ГСП-1, г. Москва, ул. Вавилова, д. 38
- ФИО
- Гарнов Сергей Владимирович (Директор)
- E-mail адрес
- office@gpi.ru
- Контактный телефон
- +7 (749) 9503873
- Сайт
- https://www.gpi.ru/