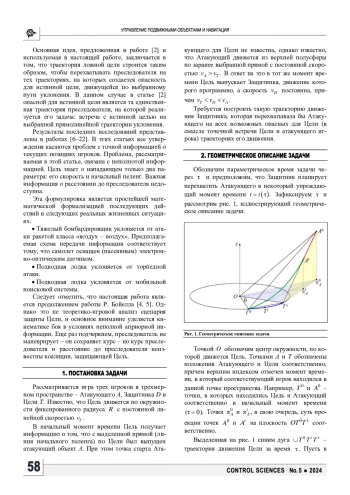
В трехмерном пространстве рассматривается ADT-игра (англ. Attacker-Defender-Target), в которой Цель (Target) совершает плоское движение по окружности с постоянной скоростью. Атакующий игрок (Attacker) движется равномерно и прямолинейно из произвольной точки верхней полусферы. Специфика постановки состоит в том, что на борту Цели имеется мобильный Защитник (Defender), в задачу которого входит перехват всех возможных опасных для Цели (в смысле точечной встречи) траекторий движения Атакующего. Задача осложняется тем, что Цель и Защитник в процессе движения не видят атакующего игрока. Им известен лишь начальный пеленг, в то время как текущий пеленг, начальная и текущая дистанции до Атакующего им не известны. По этой причине движение Цели и Защитника предполагается программным.
Идентификаторы и классификаторы
Интерес к математической формализации процессов взаимодействия мобильных объектов типа беспилотных летательных аппаратов (БПЛА) или автономных необитаемых подводных аппаратов (АНПА) в последнее время постоянно растет. Этот тренд обусловлен рядом всем известных объективных причин.
Одной из таких формализаций являются так называемые MDT- или ADT-игры (англ. Missile– Defender–Target или Attacker–Defender–Target). В них кроме традиционных для игр преследования – уклонения участников (как собственно преследователя, так и преследуемого им уклоняющегося игрока-цели) принимает участие третий игрок – Защитник. Защитник и уклоняющийся игрок-цель, действуя согласованно, образуют коалицию, которая играет против атакующего игрока. В задачу Защитника входит перехват Атакующего на траектории его движения или отвлечение Атакующего от намеченной им траектории преследования в случаях, когда Защитник играет роль ложной цели.
Список литературы
1. Ivanov, M.N., Maslov, E.P. On One Problem of Deviation // Automation and Remote Control. - 1984. - Vol. 45, no. 8. - P. 1008-1014.
2. Zheleznov, V.S., Kryakovskii B.S., Maslov, E.P. On a Catch Problem // Automation and Remote Control. - 1996. - Vol. 57, no. 8. - P. 1072-1078.
3. Rubinovich, E.Ya. Missile-Target-Defender Problem with Incomplete a Priori Information // Dynamic Games and Applications. - 2019. - Vol. 9. - P. 851-857. EDN: RYJRWC
4. Boyell, R.L. Defending a Moving Target against Missile or Torpedo Attack // IEEE Trans. Aerosp. Electron. Syst. - 1976. - Vol. AES-12, no. 4. - P. 582-586.
5. Boyell, R.L. Counterweapon Aiming for Defence of a Moving Target // IEEE Trans. Aerosp. Electron. Syst. - 1980. - Vol. AES-16, no. 3. - P. 402-408.
6. Shneydor, N.A. Comments on “Defending a Moving Target against Missile or Torpedo Attack” // IEEE Trans. Aerosp. Electron. Syst. - 1977. - Vol. AES-13, no. 3. - P. 321-321.
7. Garcia, E., Casbeer, D.W., Pham, K. and Pachter, M. Cooperative Aircraft Defense from an Attacking Missile // Proc. of the 53th IEEE Conference on Decision and Control (CDC). - Los Angeles, USA, 2014. - P. 2926-2931.
8. Pachter, M., Garcia, M., and Casbeer, D.W. Active Target Defense Differential Game // Proceedings of 52nd Annual Allerton Conference on Communication, Control, and Computing. - Allerton, 2014. - P. 46-53. EDN: URTDVJ
9. Perelman, A., Shima, T., and Rusnak, I. Cooperative Differential Games Strategies for Active Aircraft Protection from a Homing Missile // Journal of Guidance, Control, and Dynamics. - 2011. - Vol. 34, no. 3. - P. 761-773.
10. Rusnak, I., Weiss, H., and Hexner, G. Guidance Laws in Target-Missile-Defender Scenario with an Aggressive Defender // Proc. of the 18th IFAC World Congress. - Milano, Italy, 2011. - P. 9349-9354.
11. Rusnak, I. The Lady, the Bandits and the Body-Guards - a Two Team Dynamic Game // Proc. of the 16th IFAC World Congress. - Prague, Czech Republic, 2005. - P. 441-446.
12. Shima, T. Optimal Cooperative Pursuit and Evasion Strategies against a Homing Missile // AIAA Journal of Guidance, Control, and Dynamics. - 2011. - Vol. 34, no 2. - P. 414-425.
13. Yamasaki, T., and Balakrishnan, S.N. Terminal Intercept Guidance and Autopilot for Aircraft Defense against an Attacking Missile via 3D Sliding Mode Approach // Proc. of the 2012 American Control Conference (ACC). - Montreal, 2012. - P. 4631-4636.
14. Yamasaki, T., Balakrishnan, S.N., and Takano, H. Modified Command to Line-of-Sight Intercept Guidance for Aircraft Defense // Journal of Guidance, Control, and Dynamics. - 2013. - Vol. 36, no. 3. - P. 898-902.
15. Liu, Y., Qi, N., and Shan, J. Cooperative Interception with Double-Line-of-Sight-Measuring // Proceedings of the AIAAGuidance, Navigation, and Control (GNC) Conference. - Reston: American Institute of Aeronautics and Astronautics, 2013. - Art. no. AIAA 2013-5112.
16. Qi, N., Sun, Q., Zhao, J. Evasion and Pursuit Guidance Law against Defended Target // Chinese Journal of Aeronautics. - 2017. - Vol. 30, no. 6. - P. 1958-1973. EDN: YDTNGP
17. Weissyand, M., Shimazand, T., Rusnak, I. Minimum Effort Intercept and Evasion Guidance Algorithms for Active Aircraft Defense // Journal of Guidance, Control, and Dynamics. - 2016. - Vol. 39, no. 10. - P. 2297-2311.
18. Garcia, E., Casbeer, D.W., Pachter, M. Active Target Defense Differential Game with a Fast Defender // IET Control Theory and Applications. - 2017. - Vol.11, no. 17. - P. 2985-2993.
19. Garcia, E., Casbeer, D.W., Pachter, M. The Complete Differential Game of Active Target Defense // Journal of Optimization Theory and Applications. - 2021. - Vol. 191. - P. 1-25.
20. Gong, X., Chen, W., Chen, Z. Intelligent Game Strategies in Target-Missile-Defender Engagement Using Curriculum-Based Deep Reinforcement Learning // Aerospace. - 2023. - Vol. 10, no. 2. - Art. no. 133. EDN: WZLPIB
21. Галяев А.А., Самохин А.С., Самохина М.А. Моделирование отсрочки поимки цели в ADT-игре с использованием одного или двух защитников // Проблемы управления. - 2024. - № 2. - С. 83-94. EDN: GZFMGO
22. Потапов А.П., Галяев А.А. Противодействие алгоритму наведения в игре трех игроков. // Мехатроника, автоматизация, управление. - 2024. - Т. 25, № 11. - С. 575-584. EDN: RTPNIA
23. Маркеев А.П. Теоретическая механика: Учебник для университетов. - М.: ЧеРо, 1999. - 572 с. EDN: TVLORR
Выпуск
Другие статьи выпуска
Рассматриваются аналитические подходы к решению задач прокладки пути с учётом препятствий. Сравниваются два принципа аналитического моделирования препятствий на сцене: с применением метода потенциалов и путём R-функционального моделирования. Приводится принцип функционально-воксельного конструирования сложных вычислительных процессов на примере моделирования R-функции объединения или пересечения области двух функций. Разбираются основы арифметических операций над локальными геометрическими характеристиками, описывающими компоненты однородного единичного вектора локальной функции. Демонстрируется принцип денормирования таких компонент для применения в арифметических действиях, составляющих R-функцию. Рассматривается моделирование сцены в виде компоновки концентрических объектов и локальной функции описания цели поверхностью воронки в указанной точке. Рассматривается алгоритм динамического формирования итоговой локальной функции объединения поверхности воронки с поверхностью сцены в текущей точке. На основе итоговой локальной функции определяются компоненты вектора направления градиентного движения к заданной цели.
Рассмотрена модель коллективного поведения агентов в ситуации игровой неопределенности и неполной информированности. В качестве модели принятия решений агентами используется рефлексивная игра, в которой участники принимают решение на основе иерархии представлений о параметрах игры, представлений о представлениях и т. д. В центре внимания данной работы - рефлексивные игры с точечной структурой информированности и линейным наилучшим ответом игроков. Показано, что информационное равновесие в таких играх аналогично равновесию Нэша в игре на сети; в явном виде записаны выражения для равновесных ответов игроков, указаны условия существования и единственности равновесия. Приводится формулировка задачи стимулирования, аналогичной задаче стимулирования в игре на сети: показана взаимосвязь между равновесием в игре с общим знанием и равновесием в игре с неполной информированностью, в которой центр сообщает новые стимулы игрокам индивидуально.
В работе рассмотрена многоуровневая модель индикативного планирования целевых индикаторов в системе «мир (много стран) - страна - отрасли - ресурсы - мероприятия». В предлагаемой имитационной модели реализуется подход на основе сценарного планирования. Поставлена задача анализа и прогноза целевых индикаторов страны на примере показателя ВВП по ППС. Проведены оценки необходимого для реализации целевого сценария роста ВВП и валовой добавленной стоимости (ВДС) отдельных отраслей. Определены удельные показатели эффективности по финансовым и кадровым ресурсам: производительность труда и капиталоемкость. Сделана оценка необходимых для реализации целевого сценария инвестиций в основной капитал и численность занятых. Показано, что для реализации целевого сценария роста ВДС необходимы меры по ускорению роста производительности труда, выделены наиболее актуальные отрасли. В качестве исходных данных использовались данные Мирового банка и Росстата.
Рассматриваются методы формирования среднесрочного прогноза цен на финансовых и товарных рынках. Прогнозируемые процессы являются нестационарными, нелинейными, в них присутствуют структурные сдвиги, возникающие вследствие системных изменений в структуре рынка и оказывающих воздействие на него экстремальных событий. С увеличением горизонта прогноза вероятность возникновения структурных сдвигов возрастает, поэтому возникает задача прогнозирования c учетом возможных изменений в процессе на горизонте прогноза. Для прогнозирования будущих изменений рассматриваемого процесса необходимо расширение информационного поля, на котором формируется прогноз: включение экспертных суждений, результатов качественного анализа процессов, например, с применением методов фундаментального анализа, когнитивного анализа и алгоритмов их реализации. Построение среднесрочных прогнозов цен на финансовых и товарных рынках является необходимым элементом в решении задач планирования и управления социально-экономическими и производственными системами, а также в решении задач инвестиционного управления. В настоящем обзоре рассмотрены особенности прогнозируемых процессов, определяющие требования к методам формирования среднесрочных прогнозов, их реализации и отбору включаемой в прогноз информации, необходимой для обнаружения будущих изменений в процессе и причинных факторов их возникновения. Рассмотрены модели и методы статистического прогнозирования, искусственного интеллекта и фрактального анализа, а также методы, использующие в алгоритме прогнозирования информацию из различных источников: экспертных, новостных, данных поисковых систем. Проведено обобщение результатов обзора в контексте решения задачи среднесрочного прогнозирования. В заключении обозначены перспективные, по мнению авторов, направления исследований в этой области.
Статистика статьи
Статистика просмотров за 2025 год.
Издательство
- Издательство
- ИПУ РАН
- Регион
- Россия, Москва
- Почтовый адрес
- 117997, ГСП-7, г. Москва, Профсоюзная, 65
- Юр. адрес
- 117997, г. Москва, Профсоюзная, 65
- ФИО
- Новиков Дмитрий Александрович (дирек)
- E-mail адрес
- dan@ipu.ru
- Контактный телефон
- +7 (495) 3348910
- Сайт
- https://www.ipu.ru/