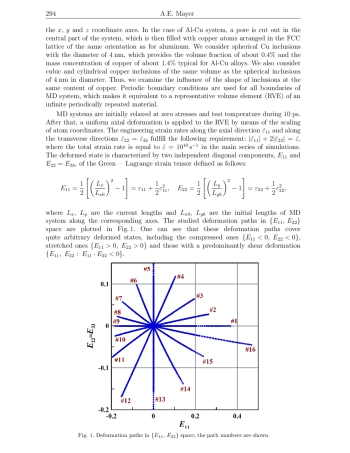
The dislocation activity controls the plastic deformation in the most of metallic materials. Mechanical loading with high strain rates or with high strain gradients can lead to either homogeneous nucleation of the dislocation or emission of dislocations from various heterogeneities, such as nanopores and phase precipitates. The dislocation nucleation and emission trigger plasticity, which relaxes the shear component of stresses. In this work, we study the threshold of dislocation emission from nanosized copper inclusions in an aluminum single crystal in comparison with the homogeneous nucleation of dislocations in pure metal. We consider different shapes of inclusions (spherical, cylindrical and cubic) and rather arbitrary axisymmetric deformations by means of molecular dynamics (MD) simulations. For most deformation paths, the copper inclusions substantially reduce the threshold of plasticity incipience, while the inclusions have no effect for some deformation paths with either axial or transverse extension. Depending on the deformation path, the shape of inclusion can either influence the emission threshold or not. Thus, there is a complex dependence of the threshold of plasticity incipience on the deformation path, the presence and the form of copper inclusions. This dependence is approximated by means of an artificial neural network (ANN) trained on the results of MD simulations. The trained ANN can be further applied as a constitutive equation at the level of continuum mechanics.
Идентификаторы и классификаторы
The dislocation activity controls the plastic deformation in the most of metallic materials. Dislocations can arise even in an ideal crystal lattice due to the process of homogeneous nucleation at strong enough elastic shear [1–6]. It is also possible the heterogeneous nucleation and emission of dislocations from various surface and bulk defects, such as grain boundaries [7–12], nanopores [13–15] and phase precipitates or inclusions [16–19]. Under normal circumstances, both homogeneous and heterogeneous nucleation is suppressed by slip and multiplication of the dislocations already existing in the material. Plasticity and relaxation of shear stresses are started by the pre-existing dislocations, and the nucleation threshold is not achieved.
Список литературы
1. Tschopp M.A., McDowell D.L. Tension-compression asymmetry in homogeneous dislocation nucleation in single crystal copper. Applied Physics Letters, 2007, vol. 90, p. 121916.
2. Aubry S., Kang K., Ryu S., Cai W. Energy barrier for homogeneous dislocation nucleation: comparing atomistic and continuum models. Scripta Materialia, 2011, vol. 64, no. 11, pp. 1043-1046. EDN: SOVOMF
3. Norman G.E., Yanilkin A.V. Homogeneous nucleation of dislocations. Physics of the Solid State, 2011, vol. 53, no. 8, pp. 1614-1619. EDN: OHQXCR
4. Xie H., Yu T., Yin F. Tension-compression asymmetry in homogeneous dislocation nucleation stress of single crystals Cu, Au, Ni and Ni3Al. Materials Science and Engineering: A, 2014, vol. 604, pp. 142-147.
5. Shehadeh M.A., Zbib H.M. On the homogeneous nucleation and propagation of dislocations under shock compression. Philosophical Magazine, 2016, vol. 96, no. 26, pp. 2752-2778. EDN: WRYBMX
6. Mayer A.E., Krasnikov V.S., Pogorelko V.V. Dislocation nucleation in Al single crystal at shear parallel to (111) plane: Molecular dynamics simulations and nucleation theory with artificial neural networks.International Journal of Plasticity, 2021, vol. 139, p. 102953.
7. Tschopp M.A., McDowell D.L. Dislocation nucleation in Σ3 asymmetric tilt grain boundaries.International Journal of Plasticity, 2008, vol. 24, no. 2, pp. 191-217.
8. Guleryuz E., Mesarovic S.D. Dislocation nucleation on grain boundaries: low angle twist and asymmetric tilt boundaries. Crystals, 2016, vol. 6, no. 7, p. 77. EDN: WSVXPF
9. Wyman R.D., Fullwood D.T., Wagoner R.H., Homer E.R. Variability of non- Schmid effects in grain boundary dislocation nucleation criteria. Acta Materialia, 2017, vol. 124, pp. 588-597.
10. Turlo V., Rupert T.J. Grain boundary complexions and the strength of nanocrystalline metals: dislocation emission and propagation. Acta Materialia, 2018, vol. 151, pp. 100-111.
11. Bobylev S.V., Enikeev N.A., Sheinerman A.G., Valiev R.Z. Strength enhancement induced by grain boundary solute segregations in ultrafine-grained alloys.International Journal of Plasticity, 2019, vol. 123, pp. 133-144.
12. Borovikov V., Mendelev M.I., King A.H. Effects of grain boundary disorder on dislocation emission. Materials Letters, 2019, vol. 237, pp. 303-305.
13. Krasnikov V.S., Mayer A.E. Plasticity driven growth of nanovoids and strength of aluminum at high rate tension: molecular dynamics simulations and continuum modeling.International Journal of Plasticity, 2015, vol. 74, pp. 75-91.
14. Feng H., Pang J., Fang Q., Chen C., Wen P. Enhanced ductility of nanomaterials through cooperative dislocation emission from cracks and grain boundaries.International Journal of Mechanical Sciences, 2020, vol. 179, p. 105652.
15. Latypov F.T., Mayer A.E., Krasnikov V. S. Dynamics of growth and collapse of nanopores in copper.International Journal of Solids and Structures, 2020, vol. 202, pp. 418-433.
16. Bryukhanov I.A., Kovalev V.L., Larin A.V. Nucleation of dislocations in aluminum alloys with copper. Physics of the Solid State, 2015, vol. 57, no. 9, pp. 1807-1817. EDN: UZWXVX
17. Bryukhanov I.A., Larin A.V. Mechanisms and rate of dislocation nucleation in aluminum-copper alloys near Guinier - Preston zones. Journal of Applied Physics, 2016, vol. 120, no. 23, p. 235106. EDN: YUWDAP
18. Pogorelko V.V., Mayer A.E. Influence of copper inclusions on the strength of aluminum matrix at high-rate tension. Materials Science and Engineering: A, 2015, vol. 642, pp. 351- 359.
19. Geslin P.-A., Gatti R., Devincre B., Rodney D. Implementation of the nudged elastic band method in a dislocation dynamics formalism: application to dislocation nucleation. Journal of the Mechanics and Physics of Solids, 2017, vol. 108, pp. 49-67.
20. Ashitkov S.I., Komarov P.S., Struleva E.V., Agranat M.B., Kanel G.I. Mechanical and optical properties of vanadium under shock picosecond loads. JETP Letters, 2015, vol. 101, pp. 276-281.
21. Zuanetti B., McGrane S.D., Bolme C.A., Prakash V. Measurement of elastic precursor decay in pre-heated aluminum films under ultra-fast laser generated shocks. Journal of Applied Physics, 2018, vol. 123, no. 19, p. 195104. EDN: VHQEZO
22. Komarov P.S., Struleva E.V., Ashitkov S.I. Generation of giant elastic ultrashort shock waves in chromium films by femto-second laser pulses. Journal of Physics: Conference Series, 2019, vol. 1147, no. 1, p. 012023. EDN: OTJCHD
23. Merkel S., Hok S., Bolme C., Rittman D., Ramos K.J., Morrow B., Lee H.J., Nagler B., Galtier E., Granados E., Hashim A., Mao W.L., Gleason A.E. Femtosecond visualization of hcp-iron strength and plasticity under shock compression. Physical Review Letters, 2021, vol. 127, no. 20, p. 205501. EDN: AYPBRL
24. Garg A., Maloney C.E. Universal scaling laws for homogeneous dislocation nucleation during nano-indentation. Journal of the Mechanics and Physics of Solids, 2016, vol. 95, pp. 742-754.
25. Zhao K., He J., Mayer A.E., Zhang Z. Effect of hydrogen on the collective behavior of dislocations in the case of nanoindentation. Acta Materialia, 2018, vol. 148, pp. 18-27.
26. Zhao K., Mayer A.E., He J., Zhang Z. Dislocation based plasticity in the case of nanoindentation.International Journal of Mechanical Sciences, 2018, vol. 148, pp. 158-173.
27. Gerold V. On the structures of Guinier - Preston zones in Al single bond Cu alloys introductory paper. Scripta Metallurgica, 1988, vol. 22, no. 7, pp. 927-932.
28. Starink M.J., Zahra A.-M. Mechanisms of combined GP zone and θ! precipitation in an Al-Cu alloy. Journal of Materials Science Letters, 1997. vol. 16, pp. 1613-1615.
29. Ma Z., Zhan L., Liu C., Xu L., Xu Y., Ma P., Li J. Stress-level-dependency and bimodal precipitation behaviors during creep ageing of Al-Cu alloy: experiments and modeling.International Journal of Plasticity 2018, vol. 110, pp. 183-201.
30. Zuiko I., Kaibyshev R. Effect of plastic deformation on the ageing behaviour of an A-Cu- Mg alloy with a high Cu/Mg ratio. Materials Science and Engineering: A, 2018, vol. 737, no. 401-412.
31. Krasnikov V.S., Mayer A.E., Pogorelko V.V., Latypov F.T., Ebel A.A.Interaction of dislocation with GP zones or θ!! phase precipitates in aluminum: atomistic simulations and dislocation dynamics.International Journal of Plasticity, 2020, vol. 125, pp. 169-190.
32. Krasnikov V.S., Mayer A.E., Pogorelko V.V. Prediction of the shear strength of aluminum with θ phase inclusions based on precipitate statistics, dislocation and molecular dynamics.International Journal of Plasticity, 2020, vol. 128, p. 102672.
33. Zuiko I., Kaibyshev R. Ageing response of cold-rolled Al-Cu-Mg alloy. Materials Science and Engineering: A, 2020, vol. 781, p. 139148.
34. Sun W., Zhu Y., Marceau R., Wang L., Zhang Q., Gao X., Hutchinson C. Precipitation strengthening of aluminum alloys by room-temperature cyclic plasticity. Science, 2019, vol. 363, pp. 972-975. Plasticity incipience in aluminum with copper inclusions 303.
35. Mayer A.E., Krasnikov V.S., Pogorelko V.V. Homogeneous nucleation of dislocations in copper: Theory and approximate description based on molecular dynamics and artificial neural networks.Computational Materials Science, 2022, vol. 206, p. 111266.
36. Mayer A.E., Lekanov M.V., Grachyova N.A., Fomin E.V. Machine-learning-based model of elastic-plastic deformation of copper for application to shock wave problem. Metals, 2022, vol. 12, p. 402.
37. Plimpton S. Fast parallel algorithms for short-range molecular dynamics. Journal of Computational Physics, 1995, vol. 117, no. 1, pp. 1-19.
38. Apostol F., Mishin Y.Interatomic potential for the Al-Cu system. Physical Review B, 2011, vol. 83, p. 054116.
39. Daw M.S., Baskes M.I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Physical Review B, 1984, vol. 29, p. 6443.
40. Mishin Y., Mehl M.J., Papaconstantopoulos D. Phase stability in the Fe-Ni system: Investigation by first-principles calculations and atomistic simulations. Acta Materialia, 2005, vol. 53, no. 15, pp. 4029-4041. EDN: NBUZEL
41. Stukowski A. Visualization and analysis of atomistic simulation data with OVITO - the Open Visualization Tool. Modelling and Simulation in Materials Science and Engineering, 2010, vol. 18, no. 1, p. 015012.
42. Stukowski A., Bulatov V.V., Arsenlis A. Automated identification and indexing of dislocations in crystal interfaces. Modelling and Simulation in Materials Science and Engineering, 2012, vol. 20, no. 8, p. 085007.
43. Stukowski A.Computational analysis methods in atomistic modeling of crystals. JOM, 2014, vol. 66, pp. 399-407.
44. Kelchner C.L., Plimpton S.J., Hamilton J.C. Dislocation nucleation and defect structure during surface indentation. Physical Review B, 1998, vol. 58, no. 17, p. 11085.
45. Hoover W.G. Canonical dynamics: Equilibrium phase-space distributions. Physical Review A, 1985, vol. 31, no. 3, pp. 1695-1697.
46. Latypov F.T., Fomin E.V., Krasnikov V.S., Mayer A.E. Dynamic compaction of aluminum with nanopores of varied shape: MD simulations and machine-learning-based approximation of deformation behavior.International Journal of Plasticity, 2022, vol. 156, p. 103363.
47. Gracheva N.A., Lekanov M.V., Mayer A.E., Fomin E.V. Application of neural networks for modeling shock-wave processes in aluminum. Mechanics of Solids, 2021, vol. 56, pp. 326-342.
Выпуск
Другие статьи выпуска
The paper presents a phenomenological generalized model of a first-order metamagnetic phase transition for the La(Fe, Si)13 compounds in the approximation of localized moments under the simultaneous action of temperature, field and pressure. To achieve the maximum cooling power of magnetic solid-state cooling devices, the Curie temperature of the working bodies should be fine-tuned by two external generalized forces: a magnetic field and pressure. The thermodynamic phenomenological models presented in the literature are mostly focused on the description of the behavior of magnetocaloric materials in the vicinity of phase transition in the absence of external pressure. In turn, the latter provide a significant reduction in the field hysteresis effect by shifting the Curie temperature and expand the working temperature range of the refrigerant. To estimate the required pressure value, a new generalized model was developed that excludes the linear dependence of the phase transition temperature on the volume change and modernizes the form of the magnetic and phonon entropy, taking into account anharmonism. In addition, the equations of state describing the behavior of working bodies underwent a multistimuli cooling cycle were obtained. The model allows estimating the upper limit of the temperature and field hysteresis and predicting the required external pressure to reduce the field hysteresis.
Исследуется отражение СВЧ-волны от слоя композитного материала из диоксида ванадия и диоксида кремния в окрестности фазового перехода полупроводник-металл. Рассчитаны зависимости коэффициента отражения от температуры, объёмной доли диоксида ванадия в композите и толщины слоя композита в области фазового перехода.
Выполнено первопринципное исследование структуры и свойств алмазоподобных углеродных нанотрубок, формируемых в процессе сворачивания алмазоподобного слоя L4. В результате расчётов методом теории функционала плотности установлено, что только алмазоподобные нанотрубки (n,0)L4, имеющие полипризматическую форму, могут устойчиво существовать. Точечная группа симметрии этих нанотрубок - n/mmm. Значение параметра трансляции находится в диапазоне от 1.6224 до 1.6342 ˚A. Молекулярно-динамические расчёты показали, что нанотрубка (5,0)L, имеющая минимальную полную энергию, должна быть устойчивой до 150 К. Изолированная нанотрубка (5,0)L4 обладает высоким значением модуля Юнга (890 ГПа) и шириной запрещённой зоны в 0.6 эВ, характерной для полупроводника. Материал на основе жгутов алмазоподобных нанотрубок (5,0)L4 с плотной упаковкой можно экспериментально идентифицировать при использовании рассчитанной порошковой рентгенограммы.
Построен алгоритм численного решения задачи кавитационного обтекания тела вращения весомой жидкостью. При совпадении направления силы тяжести и направления вертикального потока возникают новые закономерности кавитационных течений, а образующиеся при этом каверны носят название вертикальных каверн. Для вертикальных каверн возможны отрицательные значения числа кавитации, когда давление газов в каверне превосходит статическое давление в окружающей жидкости на уровне схода струй с тела. Для схематизации течения применена обобщённая схема Рябушинского. Метод решения задачи основан на методе потенциала простого слоя, который сводится к решению системы интегральных уравнений. В процессе решения определяются форма каверны и распределение скорости в жидкости в зависимости от числа кавитации и числа Фруда. Определение формы каверны проводится с помощью метода установления. Примеры расчётов приведены для диска и конусов. Выполнена оценка точности расчётов и проведено сравнение с опытными данными.
In the article the questions of unique solvability and determination of the redefinition coefficient function in the initial inverse problem for two-dimensional Whitham-type partial differential equation with impulse effects are studied. The modified method of characteristics allows partial differential equations of the first order to be represented as ordinary differential equations that describe the change of an unknown function along the line of characteristics. The unique solvability of the two-dimensional inverse problem is proved by the method of successive approximations and contraction mappings. The definition of the unknown coefficient is reduced to solving the Volterra integral equation of the first kind.
We consider local derivations on finite-dimensional Jordan algebras. We developed a technique for the description of the vector space of local derivations on an arbitrary low-dimension Jordan algebra. We also give a description of local derivations on some Jordan algebras of dimension four.
Рассматриваются неявные дифференциальные уравнения (бинарные дифференциальные уравнения) вида ap2 + 2bp + c = 0, где a = a(x, y), b = b(x, y), c = c(x, y), p =dxdXdy, причём a(0, 0) = b(0, 0) = c(0, 0) = 0. Показано, что типичное уравнение такого типа формальными заменами координат (x, y) -→ (X, Y ) приводится к формальной нормальной форме (αX + βY + γ(X))P 2 + X + Y = 0, P = dY, где α, β ∈ C \ {0}, γ -формальный ряд по переменной X, γ(0) = 0, γ,(0) = 0.
Рассматривается частный случай специальной функции Фокса. Выписаны интегральное представление, представление в виде степенного ряда, асимптотические формулы. Доказаны формулы дифференцирования целого порядка, рекуррентные и интегральные соотношения.
Исследуются вопросы разрешимости нелинейных обратных задач с зависящим от времени неизвестным элементом для эволюционных уравнений в банаховых пространствах с производными Герасимова - Капуто. Получена теорема о существовании единственного гладкого решения нелинейной задачи для разрешённого относительно старшей дробной производной уравнения с ограниченным оператором в линейной части. Она использована при исследовании вырожденных эволюционных уравнений при условии p-ограниченности пары операторов в линейной части уравнения - при старшей производной и при искомой функции. В случае действия нелинейного оператора в подпространство без вырождения доказано существование единственного гладкого решения, а при независимости нелинейного оператора от элементов подпространства вырождения показано существование единственного обобщённого решения. Полученные абстрактные результаты для вырожденных уравнений использованы при исследовании обратной задачи для модифицированной системы уравнений Соболева с неизвестными коэффициентами при младших дробных производных по времени.
Найдены все неэквивалентные представления алгебры sl2(R) в пространстве векторных полей Vect R2. Для каждого из найденных представлений описаны все обыкновенные дифференциальные уравнения, допускающие данные представления, в терминах базиса дифференциальных инвариантов и операторов инвариантного дифференцирования. Также найдены операторы Казимира соответствующей универсальной обёртывающей алгебры, проинтегрированы уравнения, порождённые оператором Казимира, и доказана алгебраическая независимость операторов инвариантного дифференцирования и оператора Казимира.
Для уравнения четвёртого порядка с постоянными коэффициентами рассмотрена одна краевая задача в прямоугольной области. Единственность решения поставленной задачи доказана методом интегралов энергии. Решение выписано через построенную функцию Грина. При обосновании равномерной сходимости установлено отличие от нуля <малого знаменателя>.
Статистика статьи
Статистика просмотров за 2025 год.
Издательство
- Издательство
- ЧЕЛГУ
- Регион
- Россия, Челябинск
- Почтовый адрес
- 454001, Челябинская обл., г. Челябинск, ул. Братьев Кашириных, д.129
- Юр. адрес
- 454001, Челябинская обл, г Челябинск, Калининский р-н, ул Братьев Кашириных, д 129
- ФИО
- Таскаев Сергей Валерьевич (РЕКТОР)
- E-mail адрес
- rector@csu.ru
- Контактный телефон
- +7 (351) 7419767
- Сайт
- https://www.csu.ru/